Introdução
Nesta oportunidade, gostaria de compartilhar aqui a transcrição de uma das aulas que ministrei recentemente no ensino médio. A aula trata de funções matemáticas aplicadas ao movimento. Falaremos tanto de movimento retilíneo uniforme quanto de movimento uniformemente variado mostrando como a linguagem matemática é utilizada para descrever o comportamento das partículas que assim se movem.
É importante considerarmos aqui a diferença entre movomento de partícula e movimento de um corpo rígido. Quando as dimensões do corpo que se movem podem ser desprezadas e não interferem em nada na análise do movimento, estamos diante de um movimento de partícula. Por exemplo, se considerarmos um caminhão que viaja em uma rodovia entre duas cidades, podemos desprezar o tamanho do caminhão e considerá-lo como uma partícula.

Quando estamos diante do trabalho de carregar um piano dentro de uma casa ou de estacionar um carro em uma vaga de estacionamento, temos o caso do movimento de corpo rígido, já que as dimensões do móvel importam.

Movimento Retilíneo e Uniforme (MRU)
Nesse tipo de movimento, a partícula se move por distâncias iguais em intervalos iguais de tempo.
Nesse caso, a velocidade é constante e diferente de zero.
\( v = constante \leq 0\)
Nosso objetivo aqui é descrever esse tipo de movimento através de três instrumentos de linguagem muito utilizados na física.
- Tabelas,
- funções algébricas e
- gráficos.
Como uma tabela pode descrever um movimento uniforme?
Vamos ver isso através de um exemplo:
Um móvel realiza um movimento uniforme num determinado referencial. Seus espaços variam com o tempo segundo os dados da tabela:
|
t(s) |
0 |
1 |
2 |
3 |
4 |
|
s(m) |
20 |
28 |
26 |
44 |
52 |
Movimento Retilíneo Uniformemente Variado (MRUV)
É um movimento em que a velocidade varia de maneira uniforme ao longo do tempo.
Nesse caso, a aceleração escalar será constante e diferente de zero.
\(a = constante \leq 0 \)Considere o seguinte exemplo.
A aceleração escalar média é definida como a razão entre a variação de velocidade e o seu respectivo intervalo de tempo.
\( a_m = \frac{\Delta v}{\Delta t}\)Existem duas importantes funções que descrevem o MRUV, são elas:
A função horária das velocidades:
\( v = v_o + a t\)e a função horária das posições:
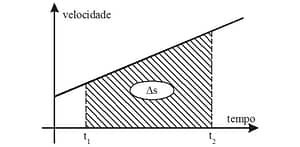
\(s = s_o + v_o t + \frac{at^2}{2} \)A função horária das posições pode ser deduzida a partir da função horária das velocidades através de cálculo integral ou simplesmente calculando a área do trapézio sob o gráfico da função das velocidades.
A expressão de Torricelli é um importante instrumento de resolução de problemas quando a questão não fornece o tempo do movimento:
\(v^2 = v_o ^2 + 2a\Delta s\)Dica bônus – baixe a apostila explicativa
Eu elaborei uma apostila explicando a relação entre os movimentos retilíneos da cinemática e as funções que estudamos na matemática. Nela, eu mostro vários exemplos usando o software geogebra e como você poderá interpretar cada coeficiente graficamente. Você poderá baixar a apostila funções e movimentos que eu elaborei para os meus estudantes do ensino médio clicando aqui.
Com essas dicas, você será capaz de relacionar a matemática com a física e compreender toda a matemática por trás do movimento na cinemática escalar.


